The conclusions reached in solving this problem using pseudo-classical techniques should give an insight with regard to how the wave function of quantum mechanics can be visualized in a manner similar to what we would use in classical mechanics; i.e., how to view and work with a cloud like distribution as if it were a classical particle, located at a point.
Finally, applying the techniques shown in this problem indicate the methods which may be used to visualize the potential function within a subatomic particle.
In classical physics, when one entity exerts an influence on another entity that would cause the entities to move, we call this influence a force, $\mathbf{F}$, which is a vector which has both magnitude and direction. Also, we describe this force as being produced by a potential, $V$, such that $\mathbf{F} = - \nabla V$ , the negative of the gradient of the potential.
The use of the symbol,$F$, expresses the magnitude of the vector $\mathbf{F}$.
From the time of Newton, it has been thought that the potential function of one infinitesimal mass, in the presence of another mass, is equal to the negative of a constant divided by the distance between the two masses. From this we can see that the force on mass $m$, in the presence of mass $M$ is given by: $F = g\,m\,M/(r^2)$, where $g$ is a constant.
Please notice that as $r$ goes to 0, the force becomes infinite. Since $F = - \nabla V$, then, $V = g\,m\,M/r$. So, the potential also becomes infinite at $r=0$ . Clearly, the Newtonian formulae are incorrect when $r$ is very close to 0.
Let us assume the existence of a large sphere with (mass) density that depends only upon the distance from the center of the sphere. This means that if we were to break up our sphere into a set of very thin concentric spherical shells, all of the matter in one shell would have the same value of density (mass per unit volume.) But the density of one shell need not be the same as the density of another shell.
For the moment, let us say that our sphere is the earth. But, this is an idealized earth as our true earth is not as uniform in density as the sphere that we want to consider.
Let us now consider a very small mass and imagine that it is a golf ball. Its size is certainly much smaller than the size of the earth, and its mass is also much smaller than that of the earth.
Also, let us say that there is a hole drilled in the earth that goes from the surface of the earth straight to the center of the earth and extending straight out on through to the other side. This hole is just large enough to pass a golf ball but it is not large enough to disrupt any of our calculations.
Our problem is to calculate the force that the earth exerts upon the golf ball. Call this the weight of gravity. Also, we want to calculate the values of the potential function that produces this force.
We want to consider what happens to the calculated value of the force and the value of the potential as the golf ball travels from an almost infinite distance from the earth, accelerates toward the earth, comes to the proximal surface of the earth, passes into the hole in the earth, passes the exact center of the earth, passes toward the distal surface of the earth, and finally passes the distal surface of the earth to proceed on its way out to infinity on the other side of the earth.
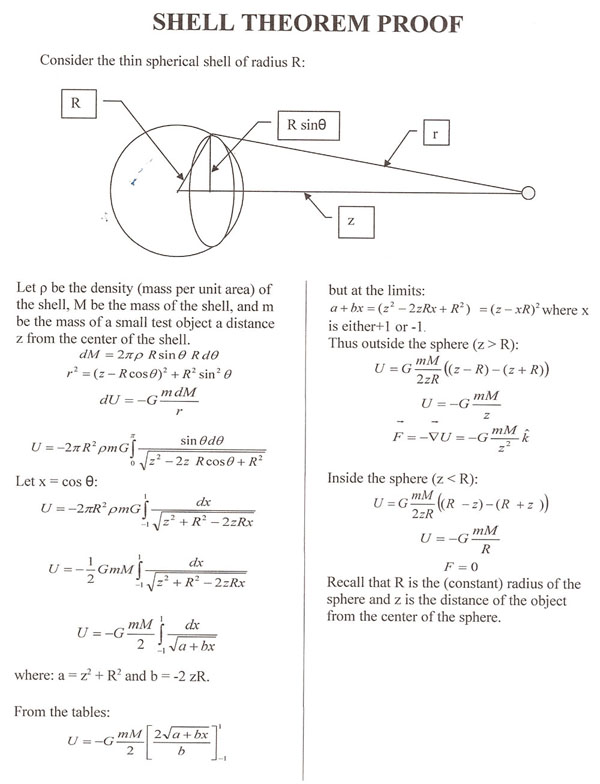
To start our search for a solution, i.e., deriving an equation that gives us a number, the force that the earth exerts upon the golf ball, let us start our solution process by considering another very small mass (another golf ball) separated from the first mass by a distance, $r$. Sir Isaac Newton told us that the magnitude of the force, $F$, exerted on each of the two masses separated by a distance $r$ is given by a simple formula. The force equals a constant times the mass of the first particle times the mass of the second particle divided by the square of the distance between the two particles. This is the very famous Newton's law of gravity.
The earth is comprised of a very large number of very small masses. Our quest is to calculate the force on the golf ball due to all of the masses of the earth. We proceed by defining an equation that expresses Newton's formula for each small mass and the golf ball. We find that this gives us three equations, as force has three directional components. So, to find the total force exerted on our golf ball, we must add all of the contributions to the force that is due to all of the very small particles that comprise the earth.
The first thing that we see is that the force is a vector quantity; that is, force has a magnitude and a direction so the formula for the force on our golf ball can be broken into three components. Two of these components are perpendicular to each other and each of these are perpendicular to the line extending from the small mass to the center of the earth. The third component is along the line to the center of the earth.
The mathematician would find that two of these integrals produce a zero result. This means that when one carries out this complicated mathematical operation of integration, we would find that the total force exerted on our golf ball by the entire mass of the earth, is directed toward the center of the earth.
If this problem were to be given to a physicist, he would say immediately that, by symmetry,the two forces perpendicular to the line extending to the center of the earth is zero because for every small particle in the earth is balanced by a counterpart mass on the other side of the earth, pulling in the opposite direction, canceling each other out. The physicist would then proceed to work out the one rather complicated integral equation, depending only upon $r$.
The formula for the force on our golf ball by the entire earth is given by a very simple formula where the force equals the product of a constant, times the mass of the golf ball, times the total mass of the earth, divided by the distance between the golf ball and the center of the earth, squared.
By using the simplified equation, we have taken a distribution of mass over a very large volume and replacing it with a single number is saying that we can visualize the solution of the problem by taking all of the mass of the earth and concentrating it at one point at the center of the earth. This statement is true even though our density function may not be the same for all values of $r$.
This problem can be extended to good advantage. Let us say that our golf ball is in the hole in the earth, so that it is somewhere in the interior of the earth. Our engineer would tell us that he has also seen that it had been worked out previously that the expression for the force on the golf ball has precisely the same form; but now the total mass of the earth that we used before must be replaced by the total mass found inside a sphere with a radius that is equal to the distance the golf ball is from the center of the earth. The contribution to the force due to mass of the spherical shells at a radius greater that the distance between the golf ball and the center of the earth cancels out! There is no net force on the golf ball that is due to all the mass at a distance from the center of the earth that is greater than the distance the golf ball is presently from the center of the earth.
One can also ask, what is the force on the golf ball if it is located far from the surface of the earth. We use the famous Newton formula. We still use the total mass of the earth as we did had the golf ball been placed on the surface of the earth.
An experienced mathematician would say that this problem has been solved and its validity has been proved. This proof is called the Shell Theorem.

Wikipedia has a nice discussion of the Shell Theorem
When the golf ball is found at a distance that is greater than (or equal to) the radius of the earth, $R$, the Newton formula holds, precisely. But, when the golf ball is inside the earth, this is no longer true.
Let us assume that the earth's mass density function is a constant. When this is so, the magnitude of the force $F$, is proportional to the mass of the earth held withing a sphere of radius $r$, which is the distance between the golf ball and the center of the earth.
The area of a spherical shell with radius $r$ is $$Area = 4 \pi r^2$$ The volume of a sphere with radius $r$: $$Volume = (4/3) \pi r^3$$ The density of the earth at radius $r$ is defined to be $$ density = \rho(r),\mbox{when}\:0 \le r \le R, 0\;\mbox{otherwise}$$
If $\rho_0$ is a constant and $$ \rho (r) \equiv \rho_0\:\mbox{when}\:0 \le r \le R, \:0\:\mbox{otherwise}$$ then, the total mass of the earth is: $$ M_R = (4/3) \pi \rho_0 R^3 $$. The mass inside a sphere of radius $r$ is: $$ M_r = (4/3) \pi \rho_0 r^3$$.
The force on the golf ball when it is at $R$: $$ F = k m M_R/ R^2 = k m (4/3) \pi \rho_0 R^3/ R^2 = k m (4/3) \pi \rho_0 R$$ The potential at $R$: $$ V = - k m (2/3) \pi \rho_0 R^2$$
The force on the golf ball at $r$, where $r$ $\le$ $R$ is $$ F = k m M_r / r^2 = k m (4/3) \pi \rho_0 r^3/ r^2 = (4/3) k m \pi \rho_0 \, r $$ The potential at $r$ is: $$ V = - (2/3) k m \pi \rho_0 \, r^2 $$
Initially, the golf ball is located a very great distance from the earth. The golf ball will experience a force of attraction toward the earth and it will accelerate in the direction of the earth. Until the golf ball reaches the proximal surface of the earth, the force increases. But, as the golf ball passes into the hole in the earth, the force will decrease. The force experienced while the golf ball is within the outer surface of the earth is directly proportional to the distance to the center of the earth.
When the golf ball is precisely at the center of the earth, the force that it experiences is identically zero. But, as its velocity is not zero, it will continue to travel outward toward and through the distal surface of the earth. At this point, its velocity will be the same as it was when it entered the proximal surface.
As the golf ball moves away from the earth, it experiences a force which is the same in magnitude as it experienced when it approached the earth (at the same distance), but the direction of the force is reversed, pointing back to the center of the earth.
Let us now pretend that the earth is miscible. This means that an infinitesimal mass would approach the earth and pass through the huge number of infinitesimal masses that comprise the earth. The same equations apply.
Before we continue, let us record the following:
When the density function is not a constant, $$ \rho = \rho(r),\mbox{when}\: 0 \le r \le R, 0\:\mbox{otherwise}. $$
The mass of a spherical shell at radius $r$: $$ dm = 4 \pi r^2 \rho(r) dr $$ The total mass of the earth, as before is: $$ M_R = (4/3) \pi R^3 \rho_0 = 4 \pi \int_0^R x^2 \rho(x) dx $$
The mass inside a sphere of radius $r$: $$ M_r = \int_0^r 4 \pi x^2 \rho(x) dx $$ And, the force on the golf ball at $r$: $$ F = k m M_r / r^2 $$
If two miscible golf balls were located at an almost infinite distance from each other, each would experience a force of attraction to the other golf ball. As the two golf balls move toward each other, pass through each other and proceed out the other side, the equations for the force and potential are the same as those given above.
Let our golf balls be represented by mass probability distribution functions; that is, by quantum mechanical wave functions. Performing the calculations to produce the values of the forces and potentials will produce expressions that are the same as the results shown, above, describing the classical problem.
The author would like to thank Dr. Kevin O'Neil, Professor of Mathematics at the University of Tulsa, Tulsa Oklahoma, for assistance and many helpful discussions with regard to the Shell Theorem.